
Both are much easier than going to C and still do quite well performance-wise. Or another vectorized implementation would be to use the broadcast function. However, you can always do this by writing the loop out yourself. The creator of is looking into using Julia’s generated functions to perform this kind of task. Even though it’s simple to see how we’d want to vectorize it, writing something that will go “okay, make A*B be a BLAS call, then call sqrt(exp()) on that” is hard to do generally. For example, sqrt(exp(A*B)) where A and B are matrices. If you want it done faster, just contribute to the github repository!. Multi-threaded will probably be added as well when it’s added to Julia’s base library. run this on GPU in parallel), OpenCL and others. What about adding Macros can take in arguments, and the developer for is looking to add a context argument so you can tell it to expand with (for multi-cpu), or even with Cuda (i.e. R = zeros (n for i = 1 : r = a * b + c * d + a endīy adding before we can get that part changed. What is does is take a vectorized expression like: There is a de-vectorization module for Julia which contains the macro.
#Matlab vectorize code
Well, a macro is simply a type of metaprogramming function that re-writes the code associated with it.
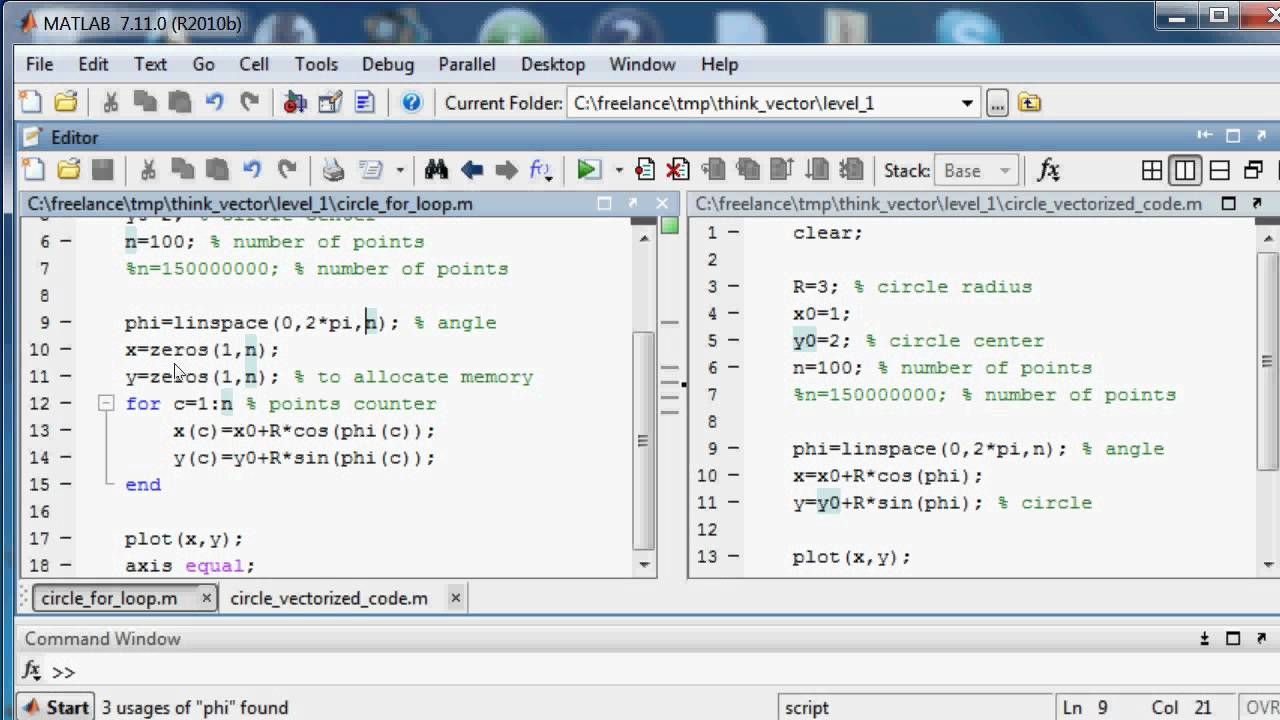
In a previous post I used macros such as without explaining what it did. What we are going to use here are macros. It is chalk-full of metaprogramming abilities. This is where Julia being a newer langugage comes to the rescue. Thus in MATLAB’s inability to metaprogram means you have to write a lot of code. …), then you will have at least a 2x slowdown in your code over written the function yourself. It also causes problems since MATLAB’s anonymous functions are notoriously slow and so if you write a function that makes a function and you make it into an anonymous function (i.e. MATLAB’s inability to metaprogram means we needed to go to C to write a loop, but that loop only works for exactly the type of inputs we had. If you aren’t familiar with metaprogramming, it is simply using programs to write programs. However, we still have the problem we noted with MATLAB that the most efficient way would be to de-vectorize and write a loop which does multiple operations at once.

With that packages you can plug it in and call the functions with ease (once vdmul gets added…). * we have to ask, can we do better? Well, the first things we can do is use MKL VML bindings in Julia. So moral of the story, A.*B uses broadcast which will beat your simple loop because of cache-control. Which shows that it speeds up the operation by storing the function in cache. * (x:: Real, r::OrdinalRange ( )įunc = get ! cache_f_na nd $gbf ($gbb, nd, narrays, f ) * ) # 26 methods for generic function ".*": However, this STILL isn’t optimal! Too see this, let us write out what MATLAB’s interpreter turns this into:
Fun! Number of Operations ~ Number of Calls Thus to do this in MATLAB you have to write some C code.
#Matlab vectorize how to
MATLAB has a page on how to use the max interface to call BLAS/LINPACK functions and using this with the v?mul (i.e. * with vector operations from MKL by directly calling MKL VML functions. How can we do better? Well, we can replace. So the simple A.*B is good for prototyping, but from benchmarking many SPDE solvers I realized this was holding me back. This is huge since processor technologies like AVX2 allows specific vector operations to do calls on 8 numbers at a time, making highly-parallel math operations like this get close to an 8x speedup if used correctly (and AVX3 is coming out soon to double that!). Another thing is that, as far as I can tell, A.*B does not have all of the processor-specific optimizations to make this operation super fast. Therefore A*B gets accelerated whereas A.*B does not. First of all, if you are using co-processors/accelerators such as the Xeon Phi, the option of automatically offloading highly-vectorized problems to a GPU-like device only offloads BLAS/LINPACK calls. these functions will run parallel on your multi-core machine), and much more!īut A.*B doesn’t do a BLAS call! When you use A.*B in MATLAB, it uses its own C-code to loop through an perform this operation. So every time you call svd, A*B, etc., you are actually calling a highly-optimized state of the art C/Fortran/Assembly code mixture which does all sorts of things to make sure you don’t have cache misses, have the function multi-threaded (i.e.


 0 kommentar(er)
0 kommentar(er)
